Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- BOJ
- 대수학
- 7469
- algebra
- 백준
- Codeforces
- 구간쿼리
- 이베이트코리아
- subgroup
- Algorithm
- ccw
- round 420
- persistent segment tree
- 이베이트
- 대한항공
- self balancing binary search tree
- 이베이트미국
- Ebate Korea
- persistent indexed tree
- Ebate USA
- 아시아나
- 알고리즘
- k번째 수
- round 424
- indexed tree
- Algebraic Geometry
- finite group
- acmicpc
- gallian
- 마일리지
Archives
- Today
- Total
[Round#419 Div.2] D. Karen and Test 본문
http://codeforces.com/contest/816/problem/D
a_1부터 a_N까지 N개의 수열이 있을 때, b_1 = a_1 + a_2, b_2 = a_2 - a_3 ... 이런 식으로 그 다음 줄에 b_n을 만든다.
같은 과정을 반복하여 수열의 수가 1개가 될 때 까지 진행했을 때 나오는 수가 뭔지 구하는 문제이다.
(말보다는 그림이 이해하기 편하니 아래그림 참조)
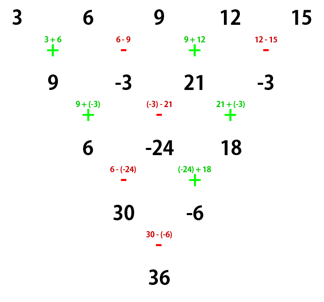
첫번째 줄 부터 계산하다 보면 4번째 줄에 와서 규칙성을 찾을 수 있는데, 바로 이항계수이다.
구체적으로 말하면, 1번째 수열들을라 하면,
5번째 줄에 나타나는 수열들은 형태를 띈다.
즉, 첫 번째 줄에 있는 수열을 라 하면,
4줄 아래있는 5번째 줄에 나타나는 수열은 이 되고,
다시 4줄 아래에 있는 9번째 줄에 나타나는 수열은 꼴이 된다.
따라서 총 N개의 수가 주어지면 계산되어지는 줄 수는 N-1줄이고, 결국 (N-1)%4 를 기준으로 이항계수를 계수로 갖는 수열들의 합을 구해주면 O(N)만에 풀어낼 수 있다.
위의 예제에서도 5번째 줄에 나타나는 수(결국엔 최종 답)는 1×3+2×9+1×15=36으로 O(N)에 구할 수 있다.
'Algorithm > CodeForces' 카테고리의 다른 글
| [Round#420 Div.2] C. Okabe and Boxes (0) | 2017.06.26 |
|---|---|
| [Round#420 Div.2] B. Okabe and Banana Trees (0) | 2017.06.26 |
| [Round#405 Div.2] B. Bear and Friendship Condition (0) | 2017.03.19 |
| [Round#404 Div.2] D. Anton and School - 2 (0) | 2017.03.16 |
| [Round#403 Div.2] B. The Meeting Place Cannot Be Changed (0) | 2017.03.11 |
