[Round#420 Div.2] B. Okabe and Banana Trees

http://codeforces.com/contest/821/problem/B

B. Okabe and Banana Trees

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Okabe needs bananas for one of his experiments for some strange reason. So he decides to go to the forest and cut banana trees.

Consider the point (x, y) in the 2D plane such that x and y are integers and 0 ≤ x, y. There is a tree in such a point, and it has x + ybananas. There are no trees nor bananas in other points. Now, Okabe draws a line with equation 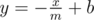. Okabe can select a single rectangle with axis aligned sides with all points on or under the line and cut all the trees in all points that are inside or on the border of this rectangle and take their bananas. Okabe's rectangle can be degenerate; that is, it can be a line segment or even a point.

Help Okabe and find the maximum number of bananas he can get if he chooses the rectangle wisely.

Okabe is sure that the answer does not exceed 1018. You can trust him.

Input

The first line of input contains two space-separated integers m and b (1 ≤ m ≤ 1000, 1 ≤ b ≤ 10000).

Output

Print the maximum number of bananas Okabe can get from the trees he cuts.

Examples

input

1 5

output

30

input

2 3

output

25

Note

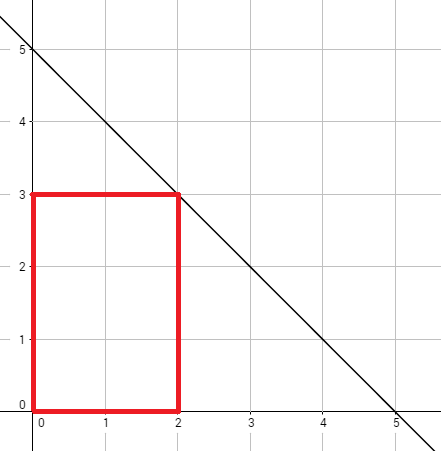
The graph above corresponds to sample test 1. The optimal rectangle is shown in red and has 30 bananas.

---

기울기가 -1/m이고, y절편이 b인 직선과 x축, y축이 이루는 삼각형 내에서 직사각형을 그려 그 직사각형이 포함하는 바나나의 최대값을 구하는 문제이다.

각 정수 좌표 (x, y)에서 x+y개의 바나나가 존재한다.

최대 바나나를 갖는 사각형의 오른쪽 위 모서리가 직선 위에 있음이 자명하므로

(0,b)에 있을 때 부터 (mb, 0)에 있을 때 까지 좌표를 하나씩 옮기며 계산해 주면 된다.

사각형의 오른쪽 위 모서리의 좌표가 (x,y)라고 한다면, 사각형이 포함하는 바나나의 개수는

(0+1+2+3+4+...+x) *(y+1) + (x+1)*(0+1+2+...+y) 이므로

x(x+1)(y+1)/2 + (x+1)y(y+1)/2 = (x+1)(y+1)(x+y)/2 가 된다.

#include <stdio.h>
#define ll long long
ll ans, cand,m,b;
int main() {
	scanf("%lld%lld", &m, &b);
	for (ll y = 0; y <= b; y++) { //x=m(b-y)
		cand = (y + 1)*(m*(b - y)*(m*(b - y) + 1) / 2) + (m*(b - y) + 1)*(y*(y + 1)) / 2;
		if (ans < cand) ans = cand;
	}
	printf("%lld", ans); 

}