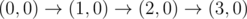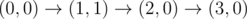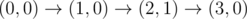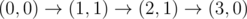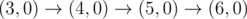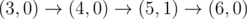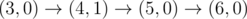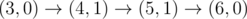[Round#420 Div.2] E. Okabe and El Psy Kongroo

http://codeforces.com/contest/821/problem/E

E. Okabe and El Psy Kongroo

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Okabe likes to take walks but knows that spies from the Organization could be anywhere; that's why he wants to know how many different walks he can take in his city safely. Okabe's city can be represented as all points (x, y) such that x and y are non-negative. Okabe starts at the origin (point (0, 0)), and needs to reach the point (k, 0). If Okabe is currently at the point (x, y), in one step he can go to (x + 1, y + 1), (x + 1, y), or (x + 1, y - 1).

Additionally, there are n horizontal line segments, the i-th of which goes from x = ai to x = bi inclusive, and is at y = ci. It is guaranteed that a1 = 0, an ≤ k ≤ bn, and ai = bi - 1 for 2 ≤ i ≤ n. The i-th line segment forces Okabe to walk with y-value in the range 0 ≤ y ≤ ciwhen his x value satisfies ai ≤ x ≤ bi, or else he might be spied on. This also means he is required to be under two line segments when one segment ends and another begins.

Okabe now wants to know how many walks there are from the origin to the point (k, 0) satisfying these conditions, modulo 109 + 7.

Input

The first line of input contains the integers n and k (1 ≤ n ≤ 100, 1 ≤ k ≤ 1018) — the number of segments and the destination xcoordinate.

The next n lines contain three space-separated integers ai, bi, and ci (0 ≤ ai < bi ≤ 1018, 0 ≤ ci ≤ 15) — the left and right ends of a segment, and its y coordinate.

It is guaranteed that a1 = 0, an ≤ k ≤ bn, and ai = bi - 1 for 2 ≤ i ≤ n.

Output

Print the number of walks satisfying the conditions, modulo 1000000007 (109 + 7).

Examples

input

1 3
0 3 3

output

4

input

2 6
0 3 0
3 10 2

output

4

Note

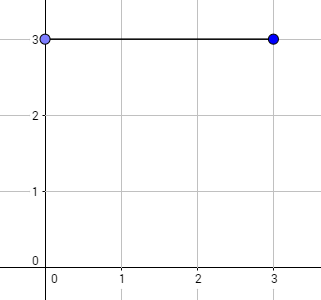
The graph above corresponds to sample 1. The possible walks are:

• 
• 
• 
• 

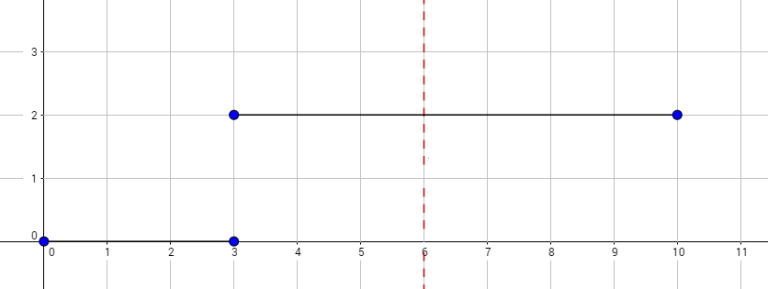
The graph above corresponds to sample 2. There is only one walk for Okabe to reach (3, 0). After this, the possible walks are:

• 
• 
• 
• 

---

x좌표가 a1~a2, a2~a3, ... , an ~ a(n+1) 인 수평선이 n개 존재할 때, 최초 (0,0)에서 시작하여 (k,0)까지 가는 경우의 수를 구하는 문제이다

다만 수평선 위로는 지나갈 수 없고, (x, y)에서 한번 이동할 때 마다 (x+1,y) or (x+1, y-1) or (x+1, y+1) 세방향으로만 이동할 수 있다.

D[i][j] = (ai, j) 까지 이동하는 경우의 수라고 정의하면

가 됨을 귀납적으로 알 수 있다. 따라서 행렬곱을 이용하면 log시간복잡도만에 DP를 계산할 수 있다.

#include <cstdio>
#include <vector>
#define MAXN 1000000007
#define ll long long
using namespace std;

ll n, k, a, b, c;
vector<vector<ll> > in;
ll cand[16], aans[16];
void calc(vector<vector<ll>> v) {
	for (int i = 0; i < 16; i++) cand[i] = 0;
	for (int i = 0; i < c; i++) {
		for (int j = 0; j < c; j++) {
			cand[i] += v[i][j] * aans[j];
			cand[i] %= MAXN;
		}
	}
	for (int i = 0; i < 16; i++) aans[i] = cand[i];
}
void make()
{
	in.clear();
	int num;
	for (int i = 0; i < c; i++) {
		vector<ll> v;
		for (int j = 0; j < c; j++) {
			if (i - 1 == j || i == j || i + 1 == j)	v.push_back(1);
			else v.push_back(0);
		}
		in.push_back(v);
	}
}
vector<vector<ll> > multipleMatrix(vector<vector<ll>> &first, vector<vector<ll>> &second)
{
	vector<vector<ll>> ans(c, vector<ll>(c));

	for (int i = 0; i < c; i++) {
		for (int j = 0; j < c; j++) {
			for (int k = 0; k < c; k++) {
				ans[i][j] += first[i][k] * second[k][j];
			}
			ans[i][j] %= MAXN;
		}
	}
	return ans;
}

vector<vector<ll>> powMatrix(vector<vector<ll>> &matrix, ll b)
{
	vector<vector<ll>> ans(c, vector<ll>(c));
	vector<vector<ll>> arr = matrix;

	for (int i = 0; i < c; i++) {
		for (int j = 0; j < c; j++) {
			if (i == j)    ans[i][j] = 1;
			else            ans[i][j] = 0;
		}
	}

	while (b > 0) {
		if (b % 2) ans = multipleMatrix(ans, arr);
		arr = multipleMatrix(arr, arr);
		b /= 2;
	}
	return ans;
}

void print(vector<vector<ll>> v)
{
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++) {
			printf("%d ", v[i][j]);
		}
		printf("\n");
	}
}

int main()
{
	aans[0] = 1;
	scanf("%lld %lld", &n, &k);
	for (int i = 1; i <= n; i++) {
		scanf("%lld%lld%lld", &a, &b, &c);
		c++;
		if (i == n) b = k;
		make();
		calc(powMatrix(in, b - a));
	}
	printf("%lld", aans[0]);
	return 0;
}